Explorando Criptografia de Reticulados

agosto 09, 2024

1. Goldreich-Goldwasser-Halevi (GGH):

O GGH é um sistema de criptografia de chave pública baseado no Problema de Vetor mais Próximo (CVP) em reticulados. Desenvolvido por Oded Golreich, Shafi Goldwasser e Shai Halevi, seu artigo foi publicado com o título “Public-key cryptosystems from lattice reduction problems.”, onde foi explorado problemas difíceis em reticulados com aplicação em criptografia e possíveis ataques ao sistema proposto.

Pouco depois, o pesquisador Phong Nguyen fez a criptoanálise do GGH, expondo que qualquer texto encriptado vaza informações da mensagem original e que uma cifra pode ser decriptada com a aproximação do Problema de Base Mais Curta, que é uma variação do Problema de Vetor mais Curto (SVP) para matrizes.

Além disso, para garantir um mínimo de segurança, a dimensão das chaves deve ser superior a 400, o que é uma grande desvantagem para o sistema, visto que teríamos que armazenar pelo menos 3 matrizes dessa magnitude.

OBS: Para acessar o conteúdo completo visite o material original

1.1. Gerando as Chaves:

O Problema de Vetor mais Próximo é resolvido sem grandes dificuldades quando temos boas bases, isto é, bases com raio de Hadamard próximo de 1. Então, é justo que essa vantagem fique com portadores da chave privada.

Para obter uma matriz com essa qualidade, primeiro gera-se $R\in\mathbb{Z}^{n\times n}$ $\{-l,\dots,+l\}^{n\times n}$ uniformemente distribuída de parâmetro$\ $$l$ onde $n$ é tamanho da mensagem. Esta é então somada a matriz $k\cdot \textsf{I}$, tal que $k=[\sqrt{n} \cdot l]$ e $\textsf{I}$ é a matriz identidade de dimensão $n$. Enquanto, o raio de Hadamard não for suficientemente próximo de 1, repita essas etapas.

$$ \textsf{V}=R+k\cdot\textsf{I} $$

Já a chave pública deve ser de ‘má’ qualidade para que qualquer um que queira solucionar o $\text{CVP}$ tenha muita dificuldade. Contudo, a chave pública $\textsf{W}$ precisa gerar o mesmo reticulado $\mathcal{L}$ que a base $\textsf{V}$ para que a mensagem encriptada possa ser decriptada.

Uma forma de garantir isso é aplicando o $\textsf{Teorema 1}$, que diz que dois reticulados $\mathcal{L}(\textsf{B})$ e $\mathcal{L}(\textsf{C})$ são iguais se e somente se existe uma matriz unimodular $U$ tal que $C=BU$. Então, precisamos gerar uma matriz unimodular para transformar a chave privada na pública. Fica à escolha do programador qual das duas formas apresentadas irá usar (Forma Normal de Hermite ou Multiplicação de Matrizes Triangulares).

$$ \textsf{W}=\textsf{U}\textsf{V} $$

Além disso, para desviar o ‘ciphertext’ do reticulado, é gerado um vetor efêmero de erros $r\in\{+\sigma,-\sigma\}^n$, onde $\sigma \in \mathbb{N}$ é o parâmetro threshold, i.e, limita o valor dos elementos do vetor. Vale ressaltar, que este valor $\sigma$ é uma informação pública, enviada juntamente com a base $\textsf{W}$.

Esse valor é calculado através da norma $l_1$ das linhas de $\textsf{V}^{-1}$. Denote $p\in\mathbb{R}^+$ como a maior norma dessas linhas, enquanto $\sigma <\frac{1}{2p}$, não há como ocorrer erros na decriptação da mensagem.

1.2. Encriptar:

O processo de encriptar uma mensagem $m$ necessita que esta seja codificada primeiro em um vetor, tal que $m\in\mathcal{F}(\textsf{V})$, i.e, o vetor da mensagem deve estar no Domínio Fundamental da Base Privada.

É interessante, que apesar do valor do threshold $\sigma$ ser público, o vetor $r$ por ele gerado não o é, visto que isso acabaria com a segurança da criptografia. Na verdade, fica na responsabilidade de quem encripta a mensagem gerar um vetor aleatório com esse valor. Esta etapa é feita escolhendo as entradas do vetor $r\in\mathbb{Z}^n$ entre $+\sigma$ e $-\sigma$ com probabilidade $1/2$.

A mensagem é então encriptada com:

$$ c= m\cdot\textsf{W}+r $$

Percebe-se então que, a dimensão das chaves pública e privada dependem exclusivamente do tamanho da mensagem.

1.3. Decriptar:

Já decriptar uma cifra é feito usando o algoritmo ‘NearestPlane’ de Babai com a chave privada $\textsf{V}$ para encontrar o vetor mais próximo de $c$. Assim, a mensagem original é obtida computando

$$ m=[c\cdot\textsf{V}^{-1}]\cdot \textsf{V}\cdot \textsf{W}^{-1} $$

Com esse novo vetor em mãos, basta decodificá-lo da mesma forma em que a mensagem foi transformada em um vetor.

Observe, que se a matriz unimodular $U$ usada para gerar a chave pública for armazenada, podemos simplificar este cálculo.

$$ m=[c\cdot\textsf{V}^{-1}]\cdot U^{-1} $$

1.4. Exemplo Prático:

Vejamos um exemplo prático com números reduzidos para facilitar compreensão:

Sejam $\textsf{V}$ a chave privada e $\textsf{W}$ a chave pública do sistema de criptografia GGH.

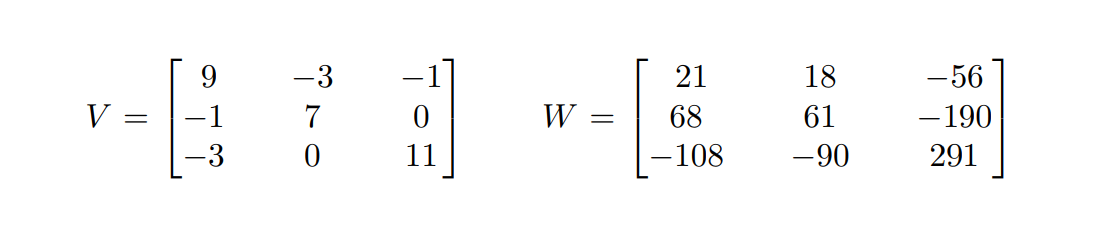
bmatrix1

Podemos verificar o quão ortogonais são essas bases com o raio de Hadamard, e de fato $\mathcal{H}(\textsf{V})\approx0.94$ e $\mathcal{H}(\textsf{W})\approx0.05$. Neste caso, threshold $\sigma$ limita os elementos do vetor efêmero $r$ em 1.

Encriptamos a mensagem $m=\text{“ABC”}$ conforme explicado e obtemos,

$$ c=\begin{bmatrix}-1383\quad-834 \quad 3317\end{bmatrix}^T $$

Em seguida para decriptar o ‘ciphertext’ é computado $[c\cdot {V}^{-1}]\cdot U^{-1}$ e encontramos o vetor $[65, 66, 67]^T$, que ao ser decodificado é transformado na string:

$$ m=\text{“ABC”} $$

1.5. Observações:

Ao longo dos anos, muitos modelos foram propostos para melhorar a segurança do GGH, como o GGH-YK e GGH-YK-M, mas cada vez mais eles se distanciavam do problema de vetor mais próximo como parâmetro de segurança, que quebra o propósito inicial da criptografia GGH.

2. Ataque de Nguyen:

Suponha que a mensagem $m\in\mathbb{Z}^n$ foi encriptada pelo GGH com a chave pública $W\in\mathbb{Z}^{n\times n}$ e o vetor de erro $r\in\{-\sigma,+\sigma\}^n$ em $c=mW+r$. A ideia principal desse ataque é reduzir $c$ em um módulo bem escolhido para que o vetor de erro $r$ possa ser eliminado da equação.

Dado que o threshold $\sigma$ é uma informação pública, a estratégia é gerar um vetor $s=\{+\sigma\}^n$ e somá-lo aos erros $r$, porque $r+s=\{0,2\sigma\}^n$.

$$ c=mW+r $$

$$ c+s=mW+r+s $$

E se dividirmos ambos os lados por $2\sigma$, a soma $r+s$ será $\{0\}^n\in\mathbb{Z}_{2\sigma}^n$ e portanto $r$ não faz mais parte da equação.

$$ c+s\equiv mW \ \ \ \ \text{(mod 2}\sigma) $$

Para solucionar esta congruência, é necessário isolar a mensagem $m$.

$$ m\equiv (c+s)\cdot W^{-1} \ \ \ \ \ (\text{mod} \ 2\sigma) $$

Na verdade este vetor $m$, não é a mensagem original, mas informações parciais dela, visto que os elementos do vetor estão reduzidos módulo $2\sigma$. Este vetor é chamado de $m_{2\sigma}$, que satisfaz $m\equiv m_{2\sigma} \ (\text{mod} \ 2\sigma)$, e portanto, existe um $m’\in\mathbb{Z}^n$ tal que

$$ m-m_{2\sigma}=2\sigma m' $$

Subtraímos o vetor $m_{2\sigma}W$ da equação de encriptação original para extrair a informação que não possuímos de $m$, para novamente dividirmos por $2\sigma$, substituindo pela forma vista acima.

$$ c-m_{2\sigma}W=(m-m_{2\sigma})W+r $$

$$ \frac{c-m_{2\sigma}W}{2\sigma}=m’W+\varepsilon $$

Perceba que o novo vetor $\varepsilon=\{-\frac{1}{2}, +\frac{1}{2}\}^n\in\mathbb{Q}^n$ transforma a norma do vetor de erros de $\sigma\sqrt{n}$ em $\sqrt{n}/2$. Apesar de ser racional, essa nova instância do CVP por Nguyen reduz muito o trabalho da procura do vetor mais próximo, até porque existem maneiras de contornar essas frações, como multiplicar ambos os lados por 2.

Nas etapas finais do ataque é usada uma técnica de incorporação, que reduz o problema em um SVP, vejamos:

Sejam o reticulado $\mathcal{L}$ gerado pela base $\textsf{B} \in\mathbb{Z}^{n\times n}$, $c$ o vetor dado no problema de $\text{CVP}$ e $\textsf{v}$ o vetor que minimiza a distância. Essa técnica incorpora o vetor $c$ na base do reticulado gerando $\mathcal{L}’$.

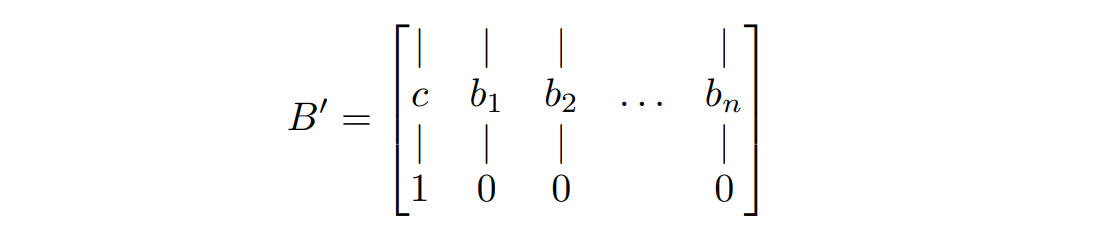
bmatrix1

O problema começa nessa parte, porque com uma jogada de fé, o algoritmo LLL de redução de base vai tentar resolver o $\text{SVP}$ de $\textsf{B}’$ e seu output vai ser $(c-\textsf{v},1)\in\mathbb{Z}^{n+1}$ que é curto e pertence a $\mathcal{L}’$, porque somente assim a instância $\text{CVP}$ de $\mathcal{L}$ é solucionada pelo $\text{SVP}$ do reticulado $\mathcal{L’}$.