Essa é a parte 1 de um estudo sobre ZKPs. A parte 2 irá conter a implementação desses protocolos utilizando Circom.
O que são Zero-Knowledge Proofs?
ZK Proofs (ou em português algo como “provas de conhecimento zero”) são o que o próprio nome diz: provas de algo ou alguma coisa que não demonstram nenhum “conhecimento” adicional ao verificador.
Um exemplo
Um exemplo bem simples pode ser visto no jogo da caverna:
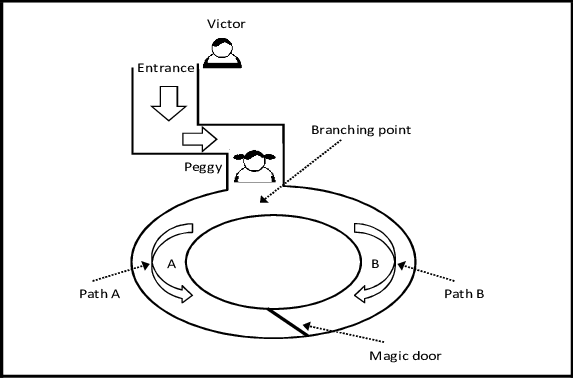
Nesse exemplo, Peggy e Victor sabem que existe uma magic door (porta mágica) que precisa de uma senha para ser aberta no meio da caverna circular. O que acontece aqui é que se Peggy escolher o caminho A e sair pela entrada do caminho B, ela teria que passar por essa porta. Dessa forma, isso prova a Victor que Peggy sabe a senha, mas ele não obtém nenhuma informação sobre ela ou qualquer outra coisa durante a interação.
Definição
Uma definição um pouco melhor é a seguinte:
Uma ZKP é um protocolo entre ($P$, $V$) (sendo $P$ o provador e $V$ o verificador) que é um algoritmo PPT (probabilistic polynomial time).
Um input público comum é o $x$ ($P$ quer provar que $x$ é, de fato, um membro de uma linguagem $L$).
Um input privado é o $W$, a witness (testemunha)
Propriedades
Completude
Se $x \in L$, $P$ possui uma testemunha $W$ correta e $(P, V)$ são honestos, $V$ vai aceitar o protocolo.
Soundness
Se $x \notin L$, $\forall$ algoritmo $P*$, $V$ vai rejeitar o protocolo com probabilidade $P$ (soundness parameter) estabelecida. Idealmente queremos $P = 1 - negl(n)$. Veja mais em negligible functions
Intuição de zero-knowledge
- O algoritmo PPT $V*$ não aprende nada com o protocolo.
- Tudo o que $V*$ aprende, $V*$ poderia ter computado sozinho.
- $\exists$ um algoritmo PPT $S$ que $V*$ poderia usar para gerar o mesmo conhecimento ($\tau$). Basicamente $S$ é um simulador.
- $\exists$ um algoritmo PPT $S$ (público) que gera uma sequência de $\tau_{sim}$ de forma que: {$\tau_{sim}$} é computacionalmente indistinguível de {$\tau_{real}$}
Protocolo de exemplo
Agora que temos uma definição um pouco mais formal, podemos olhar para um protocolo que utiliza de zero-knowledge proofs.
Isomorfismo de grafos
Sejam $G_1, G_2$ dois grafos presumidamente isomorfos. Queremos provar que sabemos um isomorfismo entre esses dois grafos sem mostrar esse isomorfismo. Vamos definir nossos parâmetros públicos como $X$, sendo ele um par de grafos $({G_0}$ e ${G_1})$. Nosso parâmetro privado (nossa testemunha ${W}$) como sendo a permutação $\Pi$ que leva ao isomorfismo entre $({G_0}$ e ${G_1})$. De forma que $G_1 = \Pi(G_0)$ e $G_0 = \Pi^{-1}(G_1)$. Chamaremos quem quer provar o isomorfismo de $P$ e o verificador de $V$.
Como o protocolo começa:
- $P$ escolhe um valor de $b$ aleatoriamente de {$0, 1$}
- $P$ computa uma permutação aleatória $\sigma$ que pode ser aplicada a qualquer um dos grafos
- $P$ calcula $G = \sigma(G_0)$ se $b=0$ e calcula $G = \sigma(G_1)$ se $b=1$.
- $P$ envia $G$ para $V$
- $V$ escolhe um valor de $b’$ aleatoriamente de ${0, 1}$ e envia para $P$
- Se $b = b’$, $P$ envia $\phi$ = $\sigma$ a $V$
- Se $b=1, b’=0$, $P$ envia $\phi$ = $\sigma \circ \Pi$
- Se $b=0, b’=1$, $P$ envia $\phi$ = $\sigma \circ \Pi^{-1}$
- $V$ recebe $\phi$ e faz a verificação:
- $G$ $\stackrel{?}{=}$ $\phi(G_{b’})$
- Se a verificação se confirmar, $V$ aceita. Caso contrário, ele rejeita
Completude
Para verificar a completude, podemos ver que se $b \neq b’$, então $\phi(G_{b’})$=$\sigma(G_b)$
Se $b = b’$, apesar de não verificarmos o isomorfismo, verificamos que $P$ não está sendo desonesto ao escolher valores de $G_0$ ou $G_1$ na hora de mandar o $G$ para $V$.
Soundness
Se $b \neq b’$ e $b’=0$, então:
$G \stackrel{?}{=} \phi(G_0)$
$G \stackrel{?}{=} \sigma \circ \Pi(G_0)$
$G \stackrel{?}{=} \sigma(G_1)$
Que se conclui como verdadeiro.
Agora para $b’=1$:
$G \stackrel{?}{=} \phi(G_1)$
$G \stackrel{?}{=} \sigma \circ \Pi^{-1}(G_1)$
$G \stackrel{?}{=} \sigma(G_0)$
Que também é verdadeiro.
Agora para $b = b’$:
Se $b = b’$, $P*$ vai falhar com uma probabilidade de 1/2. Ao rodar o protocolo várias vezes, a possibilidade de cair nesse caso é praticamente zero.
Mais formalmente temos:
Rode o protocolo $n$ vezes. Aceite a prova somente se todas as verificações forem aceitas. O soundness parameter será: $P = 1 - 1/2^n$
É importante escolhermos um valor de $\sigma$ novo a cada interação do protocolo. Se escolhermos o mesmo valor, $V*$ pode pedir o isomorfismo entre $G$ e $G_0$ e depois pedir o isomorfismo entre $G$ e $G_1$. A partir daí o verificador teria o isomorfismo entre $G_0$ e $G_1$ (yikes!).
Protocolo de identificação de Schnorr
Agora que já vimos um pouco de como funcionam as ZK-Proofs, podemos dar uma breve olhada em mais um exemplo que também é zero-knowledge.
Como funciona
Seja $E$ uma curva elíptica com ponto gerador $G$ e de ordem $q$. Suponha uma chave privada $x$ e uma chave pública $X$, sendo $X = xG$. Queremos provar o conhecimento da chave privada sem dizer mais nada sobre ela. Isto é, usando zero-knowledge.
Começamos o protocolo com o provador $(P)$ gerando um número $r$ aleatoriamente escolhido de $\mathbb{Z}_{q}$.
Depois disso, $P$ calcula $R = rG$ e envia para o verificador $(V)$
$V$ recebe o valor de $R$ e calcula um valor de $c$ aleatoriamente escolhido de um subconjunto de desafios denominado $Challenge\ space$
$V$ envia $c$ para $P$.
$P$ calcula $e = r + cx (mod\ q)$ e envia isso para $V$
$V$, por fim, multiplica $e$ por $G$ e verifica se isso se iguala a $R + cX$:
$eG \stackrel{?}{=} R + cx$
Caso ocorra uma confirmação, $V$ aceita o protocolo e acredita em $P$
Conclusão
Falaremos em mais detalhes sobre o protocolo de Schnorr na parte 2, onde utilizaremos Circom para implementar isso aí e o protocolo de isomorfismo de grafos. Até lá~ ^^
Referências
[1] https://www.youtube.com/watch?v=_MYpZQVZdiM
[2] https://en.wikipedia.org/wiki/PP_(complexity)
[3] https://www.youtube.com/watch?v=l5A3oEG-XKk
[4] Neal Koblitz. A Course in Number Theory and Cryptography
[5] Dan Boneh, Victor Shoup. A Graduate Course in Applied Cryptography
[6] Yehuda Lindell. How To Simulate It – A Tutorial on the Simulation Proof Technique
[7] Anotações de aula 18 de CS6180: Theory of computing da Cornell University
[8] Nguyen Thoi Minh Quan. Intuitive Advanced Cryptography